LA FÍSICA EN EL SIGLO XVIII ESPAÑOL. PARTE VI
José Álvarez-Cornett
No hay Reino que no sea newtoniano y, por consiguiente copernicano; mas no por eso pretenden ofender (ni aun por imaginación) a las sagradas letras que tanto debemos venerar; ¿Será decente con esto obligar a nuestra Nación a que, después de explicar los Sistemas y la Filosofía Newtoniana, haya de añadir a cada fenómeno que dependa del movimiento de la Tierra: pero no se crea éste, que es contra las Sagradas Letras? ¿No será ultrajar éstas el pretender que se opongan a las más delicadas demostraciones de Geometría y de Mecánica? ¿Podrá ningún Católico sabio entender esto sin escandalizarse?
Jorge Juan, 1773
En nuestro artículo anterior explicamos resumidamente cómo fue que las ideas de Isaac Newton se difundieron inicialmente en el continente europeo desde Inglaterra primero hacia los Países Bajos y Francia, y, posteriormente, hacia el resto de Europa. La difusión inicial se realizó, principalmente, por medio de los textos del neerlandeés Willem Jacob ‘s Gravesande, las conferencias en los Países Bajos del científico británico itinerante de origen francés John Theophilus Desaguliers, las publicaciones de Voltaire sobre Newton y la traducción al francés del Principia de Newton por la filósofa natural francesa Gabrielle Émilie Le Tonnelier de Breteuil, Marquesa de Châtelet.
Ahora, en este artículo revisaremos cómo fue la introducción en España de las ideas de la filosofía natural de Newton, el papel que jugó el padre benedictino Benito Feijjoo en la popularización de las ideas de Newton, el importante rol que cumplieron las academias militares como el Real Colegio de Artillería de Segovia y los observatorios astronómicos de la Armada española. Haremos énfasis en el papel jugado por Jorge Juan y Santacilia, oficial naval y científico de la Armada española, capitán de navío, capitán de la Compañía de Guardias Marinas de Cádiz y miembro de dos de las academias científicas más importantes del mundo (Académie Royale des Sciences de París, 1745 y Royal Society de Londres, 1749). Por otra parte, revisaremos los trabajos del matemático y astrónomo jesuita Tomás Cerdá y otros.

Retrato de Sir Isaac Newton realizado por Sir Godfrey Kneller (1702). Fuente: National Portrait Gallery, London
La difusión de las ideas de Newton en España
Recordemos que el Principia de Newton se publicó en el año 1687. En 1771, ochenta y cuatro años más tarde, la Universidad de Salamanca se manifestó a favor de la física de Aristóteles y en contra de la física newtoniana. Este rechazo es una muestra de la poca recepción de las ideas de Newton en las universidades en España en el siglo XVIII. El gobierno de Carlos III intentó hacer una renovación de los estudios universitarios. El 28 de noviembre de 1770 se expidió una Real Cédula indicándole a las universidades de Salamanca y Alcalá de Henares que debían presentar un nuevo plan de estudios. En respuesta,la Universidad de Salamanca mandó al Consejo Real de Castilla el plan de estudio indicando que:
La segunda cosa que debemos prevenir es que para dar la enseñanza de esta Facultad [de Artes], según lo que dejamos prevenido no nos podemos apartar del Sistema de Peripato [aristotélico]. Lo primero, porque dexando aparte los Filósofos antiguos, entre los que, el que merece no pequeña estimación es Platón, cuyos principios no se han adaptado bien con el común sentir; y para el uso de la Escuela, los de los Modernos Filósofos no son á proposito para conseguir los fines que se intentan por medio de este estudio. Como v.g. [verbigracia, otra forma de decir, por ejemplo] los de Neuton, que si bien disponen á el sugeto para ser un perfecto Mathematico; nada enseñan para que sea un buen Logico, y Methafísico; los de Gasendo, y Cartesio no simbolizan tanto con las verdades reveladas, como las de Aristóteles. Lo segundo, porque aun cuando no tuvieramos este tropiezo, que él solo debía bastar á excluir estos principios de las Aulas Catholicas, hallamos, que giran sus Sistemas sobre principios voluntarios, de que deducen conclusiones tambien voluntarias, é impersuasibles, como dirémos luego; y ultimamente, porque no vemos en sus Sistemas, que se estableza metodo, que descubra mayores utilidades, y adelantamientos en las Ciencias; y no siendo por este fin, nos parece escusado hacer, é introducir una novedad como esta.
En el Setecientos, en España, la mecánica newtoniana no se enseñó en el ámbito universitario sino en las academias militares, en especial, en las academias navales y en los observatorios astronómicos de la Armada española; que tenían que vérselas con el mundo real y cotidiano de la construcción de barcos, la guerra y las expediciones navales, actividades estas que requerían de conocimientos de astronomía, física y matemáticas. No obstante, la cita del jefe máximo de la Compañía de Guardias Marinas de Cádiz, el capitán de navío Jorge Juan, que presentamos al inicio también revela la dificultad que tuvieron las ciencias físicas para arraigarse en la España del siglo XVIII aún en entidades con cierto prestigio y poder como la Armada española.
En uno de nuestros artículos anteriores —La física en el siglo XVIII español. El contexto histórico —habíamos mencionado las razones por las cuales España se había cerrado al mundo europeo. En esa oportunidad dijimos que:
Después de haber hecho aportes importantes a la historia de la ciencia en el siglo XVI, debido a (i) las luchas por el poder, (ii) para evitar la entrada de las ideas protestantes, y (iii) para impedir — con poco éxito — que los secretos de las Indias se esparcieran por Europa, España [desde comienzos el siglo XVII] se cerró al mundo europeo.
Y también señalamos que:
La actividad científica en las universidades españolas fue casi nula. La universidad española, en su mayor parte en manos del estamento eclesiástico, fue muy reacia en aceptar las ideas de Copérnico y Newton prefiriendo la física aristotélica. Es por esta razón que la adopción de las nuevas ideas en la filosofía experimental en España y la difusión de la ciencia no ocurre en las universidades sino en otras instituciones como las academias militares, observatorios astronómicos de la marina, sociedades patrióticas y las instituciones que éstas crearon.
Dicho esto, sin embargo, y como lo veremos más adelante, hay que resaltar que entre las universidades españolas de la época existió una excepción: la Universidad de Valencia.
Lamentablemente, en España no se dieron intercambios científicos con Inglaterra similares al viaje de ‘s Gravesande hacia las islas británicas, la itinerancia de Desagulier desde Inglaterra hacia Holanda, travesías sobre las cuales ya comentamos en el artículo sobre la difusión de las ideas de Newton en Europa, o como el viaje a Londres, en 1715, del astrónomo francés Jacques-Eugène d’Allonville para observar un eclipse total de sol asistiendo al famoso astrónomo Edmund Halley.
Los escasos intercambios científicos, junto con la censura y la cultura del secretismo (en latín, Arcana imperii o gobernar por medio del secreto) — que fueron causa para que muchos manuscritos científicos españoles se quedaran sin ver la imprenta— y el énfasis de la sociedad española de la época en cultivar las «ciencias útiles», hicieron que la nueva filosofía natural newtoniana llegara tardíamente a España y que se difundiera muy lentamente. Sin embargo, aunque esto parezca extraño, y como lo veremos más adelante en otro artículo, España jugó un papel importante en la comprobación de la forma geométrica de la Tierra.
Dicho esto, no debe quedar en el lector la impresión de que el aislamiento científico de España desde el siglo XVII fue completo, o de que España estuvo completamente cerrada al mundo o de que fue totalmente ajena a la ciencia. Como ya presentamos en nuestros artículos sobre los novatores y sus precursores (LA FÍSICA EN EL SIGLO XVIII ESPAÑOL, I,II,III y IV), existieron individuos y grupos minoritarios, agrupados en un movimiento de renovación llamado ‘Novatores’ y un puñado de instituciones españolas que durante el siglo XVII y principios del siglo XVIII trataron de asimilar el conocimiento científico desarrollado fuera de las fronteras del Imperio español.
Pero, ciertamente, las ideas de Newton se comenzaron a estudiar tardíamente en España y las lecturas de los textos interpretativos del Principia se realizan en España solo a fines del siglo XVIII. Otra de las dificultades para la difusión de las ideas de Newton en España era que las matemáticas utilizadas en la obra de Newton, la teoría de fluxiones, lo que hoy llamamos el cálculo diferencial e integral, no eran fáciles de entender, ni aún para los matemáticos o geómetras de la época, y, en España, el conocimiento matemático estaba entonces muy poco difundido.

Retrato de Benito Jerónimo Feijoo (1676-1764) por Juan Bernabé Palomino. Fuente: Wikipedia
Benito Feijoo y la popularización de las ideas de Newton
La primera persona en España en hablarle al gran público español del Setecientos sobre las ideas de Newton fue el padre benedictino Benito Jerónimo Feijoo quien menciona al «Caballero Newton, famosísimo Matemático Inglés, y sutilísimo Filósofo», en 1728, en el Tomo II, Discurso XIV, Paradojas físicas, Paradoja IX, titulada «Es dudoso si los graves, apartados a una gran distancia de la tierra, volverían a caer en ella», y en el Discurso XV de su obra el Teatro crítico universal y también, varias veces, en su obra Cartas eruditas y curiosas publicadas entre 1742 y 1760.
No obstante, hay que aclarar que Feijoo, no leyó el Principia sino que basó su conocimiento de las ideas de Newton sobre la lectura de los textos de ‘s Gravesande. Por otra parte, la aceptación de Feijoo de las ideas de Newton fue progresiva. Al principio le puso reparos al sistema copernicano y newtoniano pero años después en otras de sus cartas eruditas los acepta. Famosa es su expresión «yo hablo como newtoniano».
En la carta 23 (Tomo II) dice:
Los elogios, que en el discurso de la Carta he dado al gran Newton, aunque muy debidos a su admirable ingenio, en ninguna manera significan alguna adherencia mía a su Sistema, el cual puedo yo justamente celebrar como ingeniosísimo, sin aceptarle como verdadero. Pero al mismo tiempo confieso, que tampoco puedo condenarle como falso; porque así para defenderle, como para impugnarle, se necesita, sobre una profundísima Geometría, una exquisita comprehensión de los Campos Celestes, de los Magnéticos, de los Eléctricos, de los Fermentativos, y otros muchos distintos de todos estos.
Pero, en la carta 23 (Tomo IV), aclara, diciendo que:
13. Los grandes progresos, que hizo el Sistema de Copérnico, se debieron en mucha parte a la extensión prodigiosa que logró en casi toda la Europa la doctrina de Newton, de cuyo Sistema Filosófico es parte esencial el Astronómico de Copérnico; de modo, que derribado éste, infaliblemente se desquicia toda la magnífica estructura de aquél.
14. Es muy de notar, que el Sistema Newtoniano halló para introducirse más contradicción en los Filósofos Franceses, que en los Italianos. Pero no se ignora la razón. Los Franceses estaban muy apasionados por su paisano Descartes; cuyos Turbillones se veían batidos en ruina por los argumentos de Newton, como asimismo la Plenitud, que Descartes atribuía al Universo; y se les hacía duro dejar al Jefe paisano por el extranjero. Al contrario, en la Italia no encontraban este obstáculo los Newtonianos, porque nunca tuvo Descartes partido en aquella Región; de modo, que en ella, impertránsito medio, se pasó de Aristóteles a Newton. Caminó, a la verdad, a paso lento por Italia el Newtonianismo; pero al fin, como ya insinué arriba, logró allí un honrado establecimiento; pues de palabra, y por escrito se enseña ya públicamente en el Colegio Romano, famosa Escuela de los Jesuitas en aquella Capital.

Fray Martín Sarmiento (1695-1772). Grabado de Francisco Muntaner, según un dibujo de Isidro Carnicero (1774). Fuente: Wikipedia.
Sin embargo, fue el padre benedictino Martín Sarmiento la primera persona en España en citar directamente al Principia y lo hace en su Demostración crítico-apologética (1732) usando la segunda edición de la obra de Newton editada y publicada, en 1713, por el profesor de astronomía del Trinity College, Universidad de Cambridge, Roger Cotes (1682-1716). La Demostración crítico-apologética es un trabajo de Sarmiento hecho en defensa de los tres primeros tomos del Teatro crítico de su amigo y colega benedictino Benito Feijoo. Aunque, según explica Antonio Reguera Rodríguez, en Newton y Feijoo. Un episodio en la historia de la difusión de las ideas científicas, Sarmiento tenía una concepción más bien cartesiana del Universo.
Sarmiento…cita los Principia de Newton… pero lo hace para descalificar tanto los supuestos teóricos como los datos concretos en los que se basaba Newton para sostener la tesis del achatamiento polar, frente a la del achatamiento ecuatorial que defendían los seguidores de Cassini en Francia. Afirma del sistema de Newton estar basado en falsedades y apoyado en medidas y datos erróneos, situándose incluso en posiciones precopernicanas. Prueba de ello es que llega a manifestar ser falsa la suposición del movimiento de la Tierra. Evidentemente no se podía ser newtoniano sin ser copernicano, y Sarmiento no era ninguna de las dos cosas.
En todo caso, debemos resaltar que ni Feijoo ni Sarmiento tenían conocimientos de matemáticas lo suficientemente profundos como para poder entender los cálculos matemáticos de Newton en el Principia. Fue en las academias militares y navales españolas en donde las teorías de Newton se estudiaron y encontraron aplicaciones.

Telescopio de reflexión del Observatorio de Madrid, de 7,6 metros (25 pies) de longitud , dotado de un espejo de 2 pies de diámetro, y el segundo en tamaño en el mundo, construido por William Herschel hacia 1796. Este observatorio y su telescopio fueron quemados y destruidos en 1808 por las tropas invasoras francesas y el edificio convertido en un polvorín (los espejos, sin embargo, fueron salvados y utilizados a principios del siglo XXI en la reconstrucción del telescopio; ver video). Fuente: Tomado de Astronomía y Navegación en el siglo XVIII, Manuel Sellés, Ediciones Akal (1992).
Jorge Juan y las academias y observatorios astronómicos de la Armada española
El conocimiento sobre la ciencia y la filosofía newtoniana que se desarrollaba en el norte de Europa se expande por la España del siglo XVIII por varios caminos o vías. Como ya señalamos, la popularización de la ciencia en la España del Setecientos estuvo a cargo de Feijoo y otros y la difusión de la ciencia por medio de su enseñanza no ocurrió en las universidades sino en otras instituciones como las academias militares, observatorios astronómicos de la marina, sociedades patrióticas y las instituciones que éstas crearon. Entre los hechos que facilitaron la transmisión de la nueva filosofía natural «con retraso a través de un penoso proceso de aculturación» están:
- El regreso a España, en 1746, de los oficiales navales y científicos de la Armada española Jorge Juan y Santacilia y Antonio de Ulloa quienes participaron de la expedición franco-española a Quito, en el Virreinato del Perú, para averiguar la forma de la Tierra; y la divulgación, en 1748, de los resultados de la expedición con la publicación del libro Observaciones Astronómicas y Physicas — esta expedición será comentada en un próximo trabajo.
- La llegada a España de varios científicos y expertos extranjeros contratados durante el reinado de Fernando VI (del 9 de julio de 1746 al 10 de agosto de 1759) entre los que se encontraban el padre jesuita checo Juan Wendlingen (1715-1790) como catedrático de matemáticas en los Reales Estudios de Madrid, el astrónomo francés Louis Goudin (1704– 1760) como profesor de matemáticas en la Universidad de San Marcos en Lima (1744-1748) y, desde 1751, como director de la Academia de guardiamarina de Cádiz y también profesor de astronomía hasta su muerte en 1760; el ingeniero militar francés Carlos Lemaur y Burriel (1724-1785) quién participó en la construcción de los canales navegables conocidos como el Canal de Castilla y el Canal de Guadarrama; el botánico y naturalista irlandés William Bowles (1705– 1780); el botánico sueco Pehr Löfling (1729-1756) quien murió durante una expedición científica en Guayana, Venezuela; y más de cincuenta técnicos navieros entre los que estaban los constructores navales Ricardo Brooth, Mateo Mullan y Edmond Bryant.
- El regreso de varias docenas de pensionados o becarios enviados al exterior (Ginebra, París y Londres) para estudiar las «ciencias útiles» principalmente, arquitectura, medicina, el arte de la relojería, y, en París, el arte de hacer grabados para realizar de mapas.

Retrato de Fray Vicente Blasco (1735-1813), rector de la Universidad de Valencia, del pintor Vicent López Portaña (1802). Fuente: Wikipedia
Enseñanza de la mecánica en la Universidad de Valencia
En 1786, la Universidad de Valencia, bajo la dirección de su rector Fray Vicente Blasco y García, logró implementar la enseñanza de la física experimental y la mecánica. El plan concebido por el Rector Blasco estructura y regula la enseñanza de la física experimental en los siguientes términos:
El Catedrático de Mecánica y Física Experimental enseñará cada año la Estática, Dinámica, Hidrostática, Hidrodinámica, Optica, Catóptrica, Dióptrica y Perspectiva. Ocupará en esta enseñanza la primera hora; y en la segunda explicará las máquinas, y hará los experimentos convenientes para dar a conocer las propiedades de los cuerpos sólidos y fluidos, especialmente del ayre, del agua, del fuego y de la luz. Se darán de lección el primer tomo del Exámen marítimo de D. Jorge Juan [ver más abajo], y las Lecciones de Optica del Abate La Caille.
El Catedrático de Astronomía ocupará hora y media en el aula enseñando cada año la Trigonometría esférica, y la Astronomía geométrica y física por las Lecciones del mismo La Caille; y en dos noches claras de cada semana ocupará una hora en el observatorio, explicando el uso de los instrumentos propios para observar, y haciendo las observaciones astronómicas que juzgue mas oportunas para la instruccion de sus discípulos.
El plan de estudio incluía la figura de «Maquinista» y un presupuesto para instrumentos. El Maquinista, que estaba a la orden de los catedráticos de Mecánica y Astronomía, era el encargado de fabricar equipos y realizar las experiencias demostrativas. En la Universidad de Valencia se construyeron máquinas según los principios del Abate Nollet, ‘sGravesande y Pieter van Musschenbroek. El primer Maquinista fue Josef Pérez, un «hábil artesano especializado en instrumentos científicos», y el primer profesor de Mecánica y Física experimental fue el valenciano Pedro Morata y Meliá quien ejerció la cátedra desde 1787 hasta su muerte en 1803. Pedro Morata creó y mantuvo el Gabinete de Física experimental de la Universidad de Valencia.

Del texto manuscrito sobre teoría de fluxiones de Tomás Cerdá. Fuente: UABDivulga.
El matemático y astrónomo Tomás Cerdá, el Real Colegio de Artillería de Segovia y la Academia de Guardias de Corps
Tomás Cerdá, también conocido como Thomas Cerda, fue un astrónomo y matemático jesuita nacido en Tarragona. Fue profesor de filosofía en Zaragoza (1747-1750) y en Cervera (en Lérida, Cataluña; 1750-1753). Refiere el historiador de la ciencia, Víctor Navarro Brotons en una entrada biográfica sobre Tomás Cerdá que:
En Cervera, Cerdá publicó un texto titulado Jesuiticae Philosophiae Theses (1753) en el que se tratan cuestiones de Física, Astronomía y Matemáticas, con referencias frecuentes a las obras de Kepler, Descartes, Gassendi, Huygens, Cassini, Clairaut, Jorge Juan, Nollet y Newton. Representa un serio intento por modernizar las enseñanzas científicas en la universidad, similar al que estaban realizando algunos profesores de la de Valencia y de alguna otra universidad española en el mismo sentido antes de las reformas de Carlos III.
En 1754, Cerdá fue enviado por la Compañía de Jesús al observatorio astronómico de la Marina de Marsella en donde estudió matemáticas con el matemático jesuita Esprit Pézenas (1692-1776), quien era el director de este observatorio y estaba familiarizado con la escuela inglesa de matemáticas basada en las ideas de Newton. A su regreso a España, en 1757, Cerdá fue nombrado profesor de la cátedra pública de matemáticas del colegio de los jesuitas de Cordelles de Barcelona (Colegio de Nobles de Santiago de Cordelles), y en 1765, se trasladó a Madrid donde se convirtió en el primer profesor de matemáticas de otro colegio jesuita, el Colegio Imperial de Madrid; para la época, este cargo llevaba asociado el puesto de Cosmógrafo Mayor de las Indias.
Cerdá estaba preocupado porque en España existían muy pocos buenos textos de matemáticas y por eso desarrolló un curso completo de «enseñanza de las Matemáticas puras y aplicadas, siguiendo la tradición enciclopedista de compendios de Matemáticas puras y mixtas o físico-matemáticas e incorporando las novedades a las diversas partes de estas disciplinas» .
Según refiere Agustín Udías, un geofísico jesuita e historiador de la ciencia, en un trabajo sobre la contribución de los jesuitas a la ciencia, inicialmente Cerdá dividió su trabajo en cinco volúmenes: aritmética y álgebra (Liciones de Matemática o Elementos Generales de Arithmética y Álgebra para el empleo de la clase), ecuaciones algebraicas, geometría y trigonometría, geometría analítica, y cálculo diferencial e integral. Cerdá fue un estudioso del cálculo de fluxiones (o como hoy se llama, cálculo diferencial e integral) y tuvo un intercambio epistolar con el matemático británico Thomas Simpson (1710-1761), autor de un famoso texto sobre fluxiones.
Para el segundo volúmen, dice Víctor Navarro Brotons, Cerdá se apoyó «en las ideas de Thomas Harriot, desarrollando los métodos de Isaac Newton y Colin Maclaurin, además de incluir las soluciones de Girolamo Cardano y Descartes a las ecuaciones de tercero y cuarto grado. Es una excelente exposición de la teoría de ecuaciones algebraicas». Entre 1758 y 1760, Tomás Cerdá publicó los primeros tres volúmenes de su curso completo. Pero, la expulsión de los jesuitas del Imperio español en 1767 impidió que se publicaran los dos últimos tomos de su obra que quedaron en forma manuscrita. Su tratado sobre fluxiones, en el cual usó como modelo el trabajo de Simpson The Doctrine and Application of Fluxions (1750), fue finalmente publicado en el año 2015 por la Real Academia de Ciencias y Artes de Barcelona (RACAB). La participación de Tomás Cerdá en la introducción del cálculo diferencial e integral en España fue objeto de estudio en la tesis doctoral de Joaquim Berenguer Clariá quien ha publicado varios artículos sobre este matemático catalán.

Portada del libro de Tomás Cerdá sobre el cálculo diferencial e integral, RACAB, 2015: Fuente: RACAB.
Quizá debido a la relación de los jesuitas con el Real Colegio de Artillería de Segovia — institución originalmente ubicada en el Alcázar de Segovia —, Cerdá proyectó publicar una serie sobre Matemáticas aplicadas que comenzó con la publicación de «Lecciones de Artillería para el empleo de la clase», obra en la que se estudia la artillería desde un punto de vista matemático.
El Real Colegio de Artillería de Segovia fue una institución fundada en tiempos de Carlos III, a iniciativa del Teniente General Félix Gazola, Conde de Gazola, Inspector y primer Director del Cuerpo de Artillería. En esta institución, abierta solo a los hijos de los nobles quienes eran aceptados desde los doce años, los cadetes recibían durante los primeros años formación en matemáticas, física y química y las aplicaciones a la artillería la recibían en el último año de estudios. En la opinión de Gazola, «La base de la teoría que necesita la Artillería es la Física, apoyada en la experiencia sobre las pólvoras, sobre los metales, sobre las maderas, etc.». Al egresar, los subtenientes estaban también capacitados para trabajar como ingenieros industriales en las fábricas militares de pólvora y cañones. El Real Colegio de Segovia es también conocido porque en él se fundó un laboratorio científico militar llamado la «Casa de la Química» dirigido, entre 1786 y 1799, por el químico francés Joseph-Louis Proust (quien enunció la ley de las proporciones definidas). El Primer Profesor (título del cargo) en el Real Colegio de Segovia fue el jesuita Antonio Eximeno Pujades quien en su discurso de inauguración se expresó diciendo que:
Dos siglos de guerra viva y continua, dice el Caballero Folard, apenas bastarán para formar sin estudio un buen Oficial. Este, como cualquier otro arte, se debe fundar en experiencias de muchos siglos. Newton, si exceptuamos el tiempo en que hizo la anatomía de la luz, apenas se llegó jamás a un instrumento de física; pero sujetando al cálculo las observaciones y experimentos ajenos, con sólo su pluma forzó, digámoslo así, a la naturaleza a que le dijera la verdad.
Se sabe que en esta institución se enseñó el cálculo diferencial e integral y la mecánica newtoniana. Es posible que Eximeno haya enseñado el cálculo diferencial e integral, sin embargo, tan solo se han encontrado documentos que comprueban la enseñanza del cálculo a partir de 1775 de manos del Primer Profesor, Cipriano Vimercati y, posteriormente, desde 1776, por un discípulo del matemático italiano Vincenzo Riccati llamado Pietro Giannini.
En relación a la serie de Matemáticas aplicadas de Cerdá, refiere Víctor Navarro Brotóns que:
Estas lecciones de artillería constituirían el sexto volumen del conjunto de la enciclopedia fisico-matemática proyectada por Cerdá (y también el último publicado como consecuencia del traslado de Cerdá a Madrid y de la expulsión de los jesuitas de España el año 1767). El séptimo correspondería a la Mecánica, el octavo sería un tratado de Hidrostática e Hidráulica, el noveno un tratado de Óptica y el décimo uno de Navegación. Se conservan también diversos manuscritos relacionados con este proyecto, entre ellos un tratado de Mecánica racional newtoniana (…), donde utiliza el cálculo diferencial, y un tratado de Astronomía. Este último es básicamente una traducción de la parte de Astronomía de la obra de Benjamin Martin Philosophia Britannica or a new system of the Newtonian Philosophy, Astronomy and Geography (1747), con algunas adiciones o cambios de Cerdá.
Cerdá influyó en la creación de la Real Academia de Ciencias y Artes de Barcelona, cuyos fundadores en su mayoría habían sido sus estudiantes. Cuando expulsaron a los jesuitas, Cerdá se fue a Forlí, en Italia, ciudad en donde murió el 18 de marzo de 1791.
También se enseñó el cálculo diferencial e integral en la Academia de Guardias de Corps, en Alcalá de Henares; los guardias de corps fueron un regimiento de guardia real que prestaba seguridad a la Familia Real. Esta academia fue una institución de duración efímera (1650-1661) pero en ella, el ingeniero militar Pedro Padilla y Arcos, director de la academia, desarrolló el Curso Militar de Matemáticas, sobre las partes de esta Ciencia, para el uso de la Real Academia establecida en el Cuartel de Guardias de Corps, en cuyo Volumen IV, basado en el libro Treatise of fluxions de Colin MacLaurin (1742), presenta el tema con el título, De la Geometría superior o de las curvas y los cálculos diferencial o integral y Método de Fluxiones (1756). Esta obra, según Elena Ausejo y Francisco Javier Medrano Sánchez, fue «el único libro de texto sobre esta materia publicado en español en este primer periodo de introducción del cálculo diferencial e integral». Recordemos que la obra de Cerdá sobre el cálculo diferencial e integral quedó inédita en el siglo XVIII.
Jorge Juan y su obra Examen Marítimo
No podemos aquí extendernos en los detalles de la vida de Jorge Juan (pero lo vamos hacer en nuestro próximo artículo), tan solo diremos que obtuvo una sólida formación científica en física, matemáticas y astronomía al estar en contacto por nueve años (1735-1744) con los científicos franceses que él acompañó en la expedición franco-española a Quito, en el Virreinato del Perú, para averiguar la forma de la Tierra (entre estos estaban Luis Godin, Charles Marie de La Condamine y Pierre Bouguer).
A su regreso a España, Jorge Juan impulsó el estudio de la mecánica newtoniana y del cálculo infinitesimal desde sus cargos en la Armada española. En particular, en la Academia de Guardias Marinas de Cádiz en donde modificó los programas de estudio para que se enseñara más física y matemáticas, trajo como profesores a Luis Godin y al cosmógrafo español Vicente Tofiño de San Miguel y editó el libro Compendio de navegación para uso de los Caballeros Guardias Marinas (1757) en el cual la navegación se enseñaba basada en las matemáticas, mecánica, astronomía, y teoría de dinámica de los fluidos. También tuvo influencia pedagógica en la Academia de Nobles Artes de San Fernando y como Director del Real Seminario de Nobles de Madrid (1770-1773) (véase, Jorge Juan: innovador de la Educación Superior en la España ilustrada). En la Academia de Nobles Artes de San Fernando, en donde se enseñaba Arquitectura, Jorge Juan contrató al matemático calatán Benito Bails (1731-1797) para que desarrollara bajo su supervisión dos libros de textos en Matemáticas, un curso grande (Elementos de matemáticas) y un curso pequeño (Principios de matemáticas). Elena Ausejo y Francisco Javier Medrano explican que:
«Los Elementos de Bails compendiaron lo más fundamental de la matemática pura y aplicada de la época. Su tercer tomo –impreso en 1772 aunque publicado en 1779–, dedicado a la aplicación del álgebra a la geometría y al cálculo infinitesimal, fue el primer texto en castellano de amplia difusión que abordó de manera extensa el cálculo diferencial e integral, adoptando la exposición continental en detrimento del enfoque fluxional. Su desarrollo está dividido en dos partes claramente diferenciadas: una introducción y un desarrollo teórico con aplicaciones.»
La obra científica más importante de Jorge Juan después de su trabajo con Antonio Ulloa, Observaciones astronómicas y phisicas hechas de orden de S. Mag. en los Reynos del Perú …de los cuales se deduce la figura, y magnitud de la Tierra y se aplica a la navegación (1748), una obra en la que ya se usaba el cálculo diferencial, es su tratado titulado «Exámen Marítimo theórico-práctico, ó tratado de Mechánica aplicado á la construcción, conocimiento y manejo de Navíos y demás Embarcaciones» (Madrid, 1771) el cual contiene un aporte original a la mecánica racional. Este texto es un riguroso tratado de mecánica aplicada a la navegación que fue traducido al inglés en 1774 y al francés por Pierre Levêque en 1783 (tuvo varias ediciones inglesas y también francesas).
En Jorge Juan y la Mecánica de los ingenieros, Manuel Sellés explica que:
El Examen se divide en dos volúmenes, de los cuales el primero se ocupa de la mecánica y el segundo de su aplicación al buque. A su vez, el primero se divide en dos libros. El Libro I contiene unos principios de mecánica general que luego se aplican al estudio de algunas máquinas, además de sendos estudios del choque y del rozamiento; en el Libro II se desarrolla una teoría de la mecánica de fluidos. De entre todos ellos se ha destacado la importancia de dicha mecánica de fluidos y de su aplicación, en el volumen segundo, al ámbito naval. El Libro I del primer volumen, hasta ahora poco estudiado, ha pasado por ser poco más que un manual al uso de mecánica aplicada. Sin embargo, como ya señalaba el mismo Juan, contenía elementos novedosos: La teoría del choque en el Capítulo VI y un estudio sobre la fricción en el VIII, que contenía, según su autor, «una nueva theorica.
Examen marítimo fue traducido al francés, en 1783, por Pierre Leveque (también al inglés, en Londres, en 1784, y al italiano en 1818) quien dijo que: «ninguna de las teorías presentadas hasta aquí ha proporcionado resultados tan conformes con la experiencia». A este comentario hay que añadirle los elogios del astrónomo Jérôme Lalande: «El Examen marítimo contiene la mejor teoría de la resistencia de los fluidos, de la construcción y de la maniobra de los navíos; es uno de los mejores libros de mecánica aplicada a la marina; y no sería exagerado recomendar su uso a los que son amantes de la ciencia».
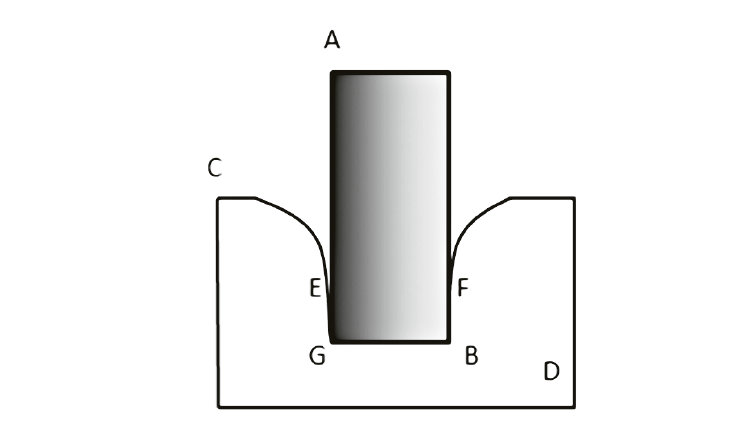
Gráfico de la impronta del choque de un cilindro contra una superficie plana mostrando la deformación de la misma. Fuente: Según la Figura 24 del tomo I de Examen marítimo en la versión modificada que aparece en el trabajo de Manuel Sellés.
En este trabajo, Jorge Juan realizó un tratamiento analítico muy novedoso para mil setecientos sobre la mecánica de contacto o choques (elástico e inelástico) y sobre la teoría de rozamiento (fricción). La novedad del estudio sobre choques de Jorge Juan, nos dice Manuel Sellés, «radica en la consideración de que no hay choques instantáneos y en la de que los cuerpos perfectamente duros constituyen un límite inalcanzable para los cuerpos que se encuentran en la naturaleza».
Según Manuel Sellés:
«Más o menos lo mismo podría decirse de su teoría del rozamiento. El trabajo verdaderamente influyente del siglo XVIII fue el llevado a cabo por Ch. A. Coulomb en 1781. Pero éste fue fundamentalmente de carácter experimental. De nuevo el trabajo de Juan destaca como el tratamiento analítico más completo, superando en esto al de Euler. Visto retrospectivamente, pudo equivocarse respecto de la existencia de un coeficiente de rozamiento cinético. Pero por otra parte anticipó otros resultados descubiertos por Coulomb. Uno, que la fricción estática aumenta con el tiempo de reposo hasta alcanzar un límite, lo que Juan hubiese explicado como un efecto de la presión, que habría ido formando una impresión hasta detenerse ésta al alcanzarse un estado de equilibrio. La segunda es la independencia de la fricción cinética de la velocidad, permaneciendo la misma a diferentes velocidades, una ley que se atribuye a Coulomb aunque éste constató que no se cumplía en todos los casos. Además Juan estuvo acertado respecto de la dependencia directa de la fuerza de fricción con la magnitud de las escabrosidades, es decir, con el área real de contacto. Este área real aumenta proporcionalmente a la fuerza normal, por lo que la simple proporcionalidad directa entre la superficie del cuerpo y la fuerza de rozamiento resulta más o menos independiente de dicha superficie»
El amplio rango de influencia de Jorge Juan en la vida de España hace que su persona sea de esas a quienes se le puede aplicar aquella frase dicha por Antonio Lafuente y José Luis Peset (en Las actividades e instituciones científicas en la España ilustrada): «algunas personas logran tanta influencia y eficacia para sus propuestas que casi cabría considerarlas como instituciones de la vida cultural y científica española».
En nuestro próximo artículo trataremos el tema de la participación del Imperio español en la solución del problema de la forma de la Tierra y veremos el rol que jugaron los militares y científicos españoles Jorge Juan y Antonio de Ulloa.
Para saber más
La obra principal de Benito Feijoo está representada por su Teatro crítico universal, ocho volúmenes publicados entre 1726 y 1740, y por los cinco volúmenes de las Cartas eruditas y curiosas (166 ensayos, más cortos que los del Teatro…), publicados entre 1742 y 1760. Las menciones a Newton en las Cartas ocurren en el Tomo II, carta 23, «Sobre los sistemas filosóficos», Tomo III, carta 20, sobre el sistema copernicano; Tomo IV, carta 21, progresos del sistema filosófico de Newton y del astronómico de Copérnico.
La enseñanza de la física en la Universidad de Valencia se presenta en Antonio Ten (1983). La física experimental en la Universidad española de fines del siglo XVIII y principios del XIX: la Universidad de Valencia y su Aula de Mecánica y Física Experimental. Llull: Revista de la Sociedad Española de Historia de las Ciencias y de las Técnicas, 6(10), 165-190. Ver también, Plan de estudios aprobado por S. M. y mandado observar en la Universidad de Valencia.
Sobre los jesuitas y la ciencia y en especial sobre el matemático Tomás Cerdá se pueden leer los trabajos de Agustín Udías (Jesuit Contribution to Science. A History, Springer, 2015) y los trabajos del historiador Joaquim Berenguer Claría (Tomàs Cerdà: introductor de la teoría de fluxiones, Suma, noviembre, 2016) y su tesis doctoral (en catalán) titulada: La Recepció del càlcul diferencial a l’Espanya del segle XVIII Tomàs Cerdà: introductor de la teoria de fluxions.
Un perfil biográfico de Jorge Juan y Santacilia se puede leer en el portal Cervantes virtual. En relación a su contribución a la difusión del cálculo en España, véase Elena Ausejo y Francisco Javier Medrano Sánchez en Jorge Juan y la consolidación del cálculo infinitesimal en España (1750-1814).
Sobre el Examen Marítimo theórico-práctico, véase Jorge Juan y la Mecánica de los ingenieros de Manuel Sellés. La obra original de Jorge Juan Examen marítimo se presenta en dos tomos y se puede consultar en los siguientes enlaces: Tomo 1 y Tomo 2.
José Álvarez-Cornett es Licenciado en Física (Universidad Central de Venezuela (UCV), 1981) con posgrados en Geociencias (Universidad de California, Berkeley) y Negocios (MBA, University of Southern California, 2000). Es geofísico petrolero, especializado en planificación estratégica y negocios Asia-Pacífico, estudió mandarín y cultura china en el Beijing Language and Cultural University (1992-1995). Ensayista, especialista en curaduría de contenidos – web information advisory – y estrategias de infoatención, profesor universitario (UCV) de historia de la ciencia y la tecnología. Fue colaborador invitado en el Laboratorio de Historia de la Ciencia y la Tecnología del Centro de Estudios de la Ciencia del Instituto Venezolano de Investigaciones Científicas (IVIC) (Abril 2016 a Septiembre 2018). Es investigador principal del Proyecto VES. Además de la historia de la ciencia y la tecnología, está interesado en la cultura y culinaria asiática, el desarrollo sostenible, la prospectiva tecnológica y los futuros personales. Está en Twitter: @Chegoyo
AGRADECIMIENTOS
La Fundación Persea agradece la infinita generosidad de sus patrocinadores: Carlos Ortega Sr., Sobella Mejías, Solmar Valera, Jiří Svozilík, Héctor Pittman Villarreal, My fit body project y Vicente Di Clemente.







0 comentarios